
Answers (For Guiding Purposes)
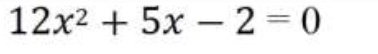
To solve the quadratic equation 12x^2 + 5x− 2 = 0 We must first determine the values of a, b, and c in the generic quadratic equation form, which is, using the quadratic formula, ax^2 + bx + c = 0.
Here, a = 2, b = 5, and c = -2.
The quadratic formula is:
= (−b ± √b^2 − 4ac) / 2a
Substituting the values of a, b, and c in the quadratic formula, we get:
= (−5 ± √5^2 − 4(2)(−2)) / 2(2)
= (−5 ± √41) / 4
Therefore, the solutions to the quadratic equation 2x^2 + 5x − 2 = 0 are = (-5 + √41) / 4 or
= (-5 – √41) / 4.
Due to the discriminant’s value being higher than zero than the square root in the quadratic formula, these roots are not equivalent.